La fonction VPM d'Excel permet de calculer les mensualités d'un emprunt. Ses paramètres sont
- Le taux
Taux d'intérêt de l'emprunt (attention à la période utilisée)
- NPM
Le nombre de remboursements pour l’emprunt.
- VA
La valeur actuelle, c'est le prix du bien acheté
- VC
La valeur capitalisée. Ne sert que pour les calculs de placement avec somme à retirer à la fin de l'investissement.
- Type (0 ou 1)
Selon le cas si les remboursements sont fait au début (1) ou à la fin (0) de la période
La fonction VPM est la traduction de Valeur de PaieMent.
=VPM(taux;npm;va;vc;type)
Utilisation de la fonction VPM
Prenons le cas d'un emprunt de 50 000€ sur 15 ans au taux de 4%.
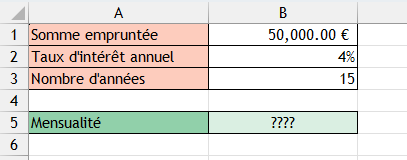
Faire le calcul avec la fonction VPM
La formule est la suivante :
=VPM(4%;15;50000) => -4 497,06 €
La fonction retourne TOUJOURS une valeur négative car il s'agit d'un décaissement. Mais il est très facile de retourner le résultat positivement soit en multipliant par -1 soit avec la fonction ABS (valeur absolue).
=VPM(4%;15;50000)*-1
=ABS(VPM(4%;15;50000))
Mais attention aux erreurs d'interprétation. Ce résultat, c'est le versement annuel et pas mensuel. Alors comment calculer des mensualités ? Pour que la fonction VPM retourne une mensualité, il faut transformer la durée de l'emprunt et le taux d'intérêt.
Changer le nombre de périodes sur 12 mois
La première chose importante à réaliser c'est d'indiquer comme valeur le nombre de périodes, le nombre de mois et non pas d'années. Le calcul très simple
=nombre d'années*12
Transformer le taux d'intérêt annuel en taux mensuel
C'est LA QUESTION la plus importante car le calcul dépend de la nature du prêt ?? En France, le calcul sera différent selon la nature du prêt
- Soit un prêt immobilier
- Ou un prêt de consommation courante
#1 : Méthode pour le calcul du taux sur un prêt immobilier (simple)
C'est la méthode de calcul la plus simple. Il suffit de diviser le taux d'intérêt annuel par 12 (le nombre de mois dans l'année).
=Taux d'intérêt/12
#2 : Méthode pour le calcul du taux pour un prêt de courte durée (compliquée)
Le calcul ici est plus complexe car il faut prendre en compte les remboursements sur chaque mois. La formule qui permet de convertir un taux annuel en taux mensuel est
=PUISSANCE(1+taux annuel;1/12)-1
ou
=(1+taux annuel)^(1/12)-1
Le 1/12 c'est pour les 12 mois (cf. l'article sur le calcul de la racine cubique). Si vous voulez convertir en taux trimestriel, il faut écrire 1/4.
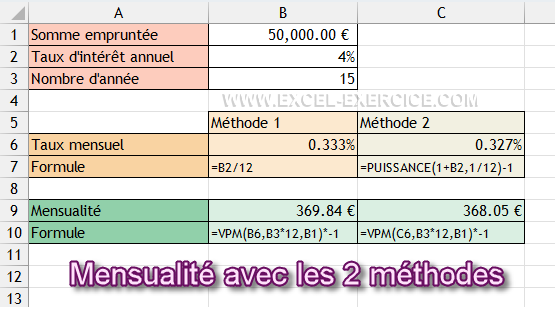
Calcul des mensualités
Nous avons recalculé le nombre de périodes ainsi que le taux d'intérêt mensuel. Nous avons tous les arguments pour renseigner la fonction VPM. Pour reprendre notre exemple, le calcul du montant des mensualités s'obtient avec la formule suivante :
=VPM((1+4%)^(1/12)-1;15*12;50000)*-1
Par défaut, VPM retourne une valeur négative. Pour retourner un résultat positif, il suffit de multiplier la formule par -1
Articles liés
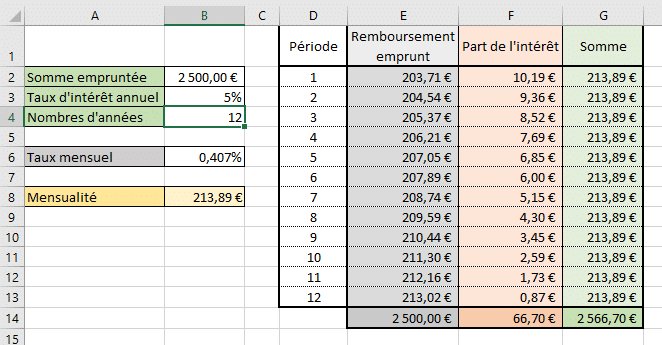
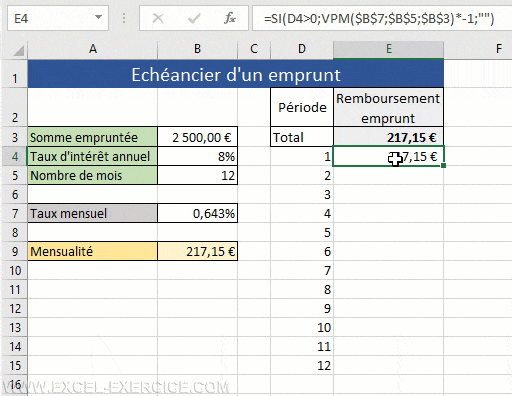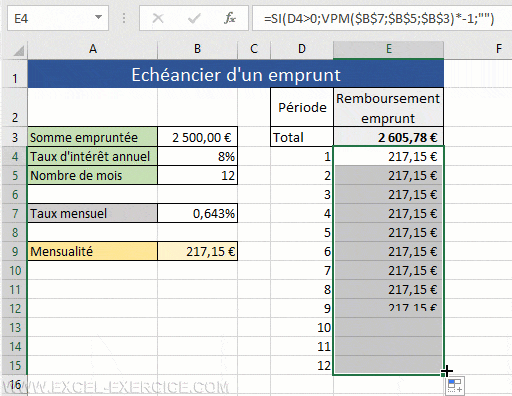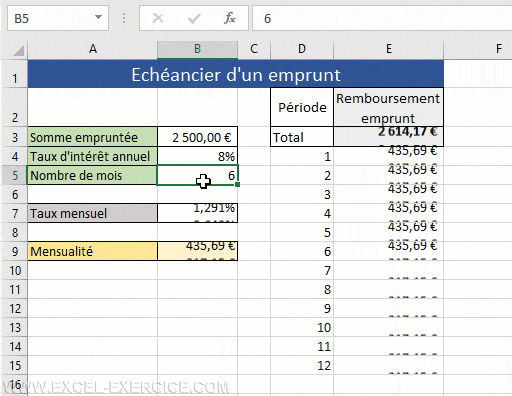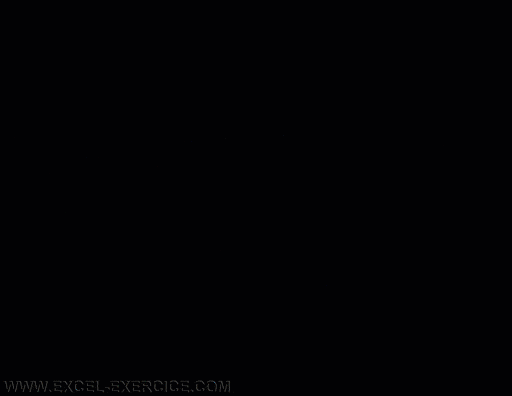
- Construction d'un échéancier d'emprunt dynamique (les mensualités sont recalculées immédiatement grâce à la fonction SEQUENCE)


30/10/2023 @ 16:10
Merci très instructif
04/09/2023 @ 19:58
Calcul des mensualités
Nous avons recalculer le nombre de périodes ainsi que le taux d'intérêt mensuel. Nous avons tous les arguments pour renseigner la fonction VPM
☹
Nous avons recalculé ...
28/05/2023 @ 16:39
Tous ces calculs savants n'expliquent pas pourquoi la fonction VPM de Excel ne donne pas le même résultat que les calculatrices hypothécaires en ligne.
Si je demande un emprunt hypothécaire à la banque, ils ne vont pas utiliser Excel pour faire le calcul mais leur propre calculatrice comme celles affichées en ligne..
29/05/2023 @ 08:55
Bonjour, il faudrait me donner plus d'éléments pour comprendre le problème que vous évoquez. La formule VPM est correcte. Pour preuve, il suffit de faire la somme des mensualités pour voir que les résultats sont justes.
C'est quoi votre simulateur ? C'est quoi vos données d'emprunt ?
21/09/2021 @ 23:21
Bonjour,
Quelle est la formule à appliquer dans ce cas-ci
J'emprunte 25 000 $, mon taux d'intérêt est de 3% par mois et ce sera le même tous les mois et je dois rembourser la totalité en 5 mois.
Merci
22/09/2021 @ 11:37
Ben, la même formule que celle expliquée dans l'article
25/02/2021 @ 19:20
Bonjour,
Je cherche à modeliser un emprunt avec une partie amortissable et une partie bullet. Est ce que vc dans la formule VPM correspond à la portion bullet du prêt?
MErci de votre aide, je ne sais pas trop comment modéliser si ce n'est en séparant le prêt en deux!
Hortense
17/02/2021 @ 07:02
Bonjour,
Une précision :
"Beaucoup d'articles vous disent que pour convertir un taux annuel en taux mensuel il suffit de diviser le taux par 12. Ce n'est pas exact car le taux cours d'un mois sur l'autre et donc le montant à rembourser sont recalculés chaque mois."
Je suis bien d'accord avec vous, cette formule a la vie dure. Ce calcul correspond à une moyenne arithmétique, en référence aux suites arithmétiques ; ce taux n'est qu'approximatif, il s'appuie sur la relation (1+t)^n≈1+nt lorsque t est faible.
La formule =PUISSANCE(1+taux annuel;1/12)-1 donne la moyenne géométrique, en référence aux suites géométriques, ce calcul est exact. Je suppose que le premier calcul a été longtemps utilisé par le passé car on ne disposait pas de moyens suffisants pour calculer une racine 12e.
19/01/2021 @ 15:24
Bonjour,
Merci pour ces explications très claires. Il reste un élément que je ne comprends pas : pourquoi si l'on prend la cellule C10 (calcul officiel) et qu'on la multiplie par 12 pour retrouver des annuités, on obtient un chiffre différent (4 416€) du montant d'annuité.
En d'autres termes, pourquoi sur excel on a l'inégalité suivante : =VPM (4%;15;50000) différent de =VPM((1+4%)^(1/12)-1;15*12;50000)*12 .
21/01/2021 @ 15:25
C'est tout simplement parce que ce n'est pas la même égalité. La première formule 4%;15;50000 considère que le 4% c'est le taux constant sur l'année et la deuxième formule réajuste tous les mois les mensualités après chaque mensualités versées. Je sais que la différence n'est pas simple à comprendre mais c'est le principe des mathématiques financières
27/10/2020 @ 16:08
Bonjour Monsieur, je comprend mais quelque souci au niveau du résultat qui m'affiche en EURO peut-on convertir en FCFA SVP. Merci!
03/07/2020 @ 17:23
Bonjour,
Merci pour cette formule qui fonctionne bien pour un taux supérieur à 1%
Je bloque avec un taux d'assurance à 0.29% pour lequel votre formule (et ce que j'ai pu essayer de mon côté) ne fonctionne pas.
Auriez-vous une solution ?
03/07/2020 @ 18:40
Bonjour,
Quelle formule ? Celle du calcul des mensualités ou du taux mensuel ?
04/07/2020 @ 08:30
Et je m'aperçois qu'en renseignant les cases via l'onglet formule / financier / VPM le résultat est le même.
C'est Excel qui bloque
04/07/2020 @ 08:57
Et au final à force de me creuser la tête il est possible que le montant mensuel de l'assurance ne soit pas pris sur la capitale emprunté...